第六章 凸轮机构

一、基本要求

凸轮机构是一种由凸轮、从动件（也称推杆）和机架组成的高副传动机构，是常用的典型机构之一，具有结构简单紧凑、控制准确有效、运动特性好、使用方便、适应性强、性能稳定以及可实现复杂的运动规律等优点，广泛地应用于发动机、轻工、纺织、造纸、服装和印刷等工业领域。

本章主要介绍凸轮机构中从动件的运动规律及凸轮轮廓曲线的设计与分析等内容，其教学基本要求如下：

（1） 了解凸轮机构的组成、类型及应用。

（2） 了解从动件常用的运动规律及特点，并学会如何选择或设计从动件的运动规律。

（3） 深刻理解相对运动（也称“反转法”）原理，并能利用该原理设计盘形凸轮的轮廓曲线（图解法）。

（4） 掌握用解析法设计盘形凸轮的轮廓曲线。

（5） 能正确确定凸轮机构的压力角、基圆半径和滚子半径等基本尺寸。

二、基本概念和基础知识

1．基本概念

（1）凸轮机构的基本名词术语 凸轮机构的基本名词术语如下：

① 基圆 以凸轮的回转中心为圆心，凸轮轮廓的最小向径为半径所作的圆，称为凸轮的基圆，它是设计凸轮轮廓曲线的基准，基圆半径用表示。

② 推程 从动件从距凸轮回转中心的最近点向最远点运动的过程。

③ 回程 从动件从距凸轮回转中心的最远点向最近点运动的过程。

④ 行程 从动件从距凸轮回转中心的最近点运动到最远点所通过的距离，或从最远点回到最近点所通过的距离。行程是指从动件的最大运动距离，常用h来表示。

⑤ 推程运动角 从动件从距凸轮回转中心的最近点运动到最远点时，对应凸轮所转过的角度称为推程运动角，用表示。

⑥ 回程运动角 从动件从距凸轮回转中心的最远点运动到最近点时，对应凸轮所转过的角度称为回程运动角，用表示。

⑦ 远休止角 从动件在距凸轮回转中心的最远点静止不动时，对应凸轮所转过的角度称为远休止角，用表示。

⑧ 近休止角 从动件在距凸轮回转中心的最近点静止不动时，对应凸轮所转过的角度称为近休止角，用 表示。

⑨ 凸轮转角 凸轮绕自身轴线转过的角度，称为凸轮转角。一般情况下，凸轮转角从行程的起始点在基圆上开始度量，其值等于行程起点和从动件的运动方向线与基圆的交点所组成的圆弧对应的基圆圆心角。

⑩ 从动件的位移 凸轮转过转角j时，从动件所运动的距离称为从动件的位移。通常，位移s从距凸轮回转中心的最近点开始度量。对于摆动从动件，其位移为角位移。

（2）从动件的运动规律 凸轮机构中，从动件的运动规律是指从动件的位移s、速度v、加速度a与凸轮转角j （或时间t）之间的函数关系，可以用方程表示，也可用线图表示。从动件运动规律的一般方程表达式为：s= s (j) ，v=v (j) ，a=a (j)。 而从动件的位移、速度和加速度与凸轮转角（或时间）之间的关系曲线分别称为从动件的位移曲线、速度曲线和加速度曲线，统称为从动件的运动规律线图。

凸轮一般为凸轮机构的主动件，且作匀速回转运动。设凸轮的角速度为，则从动件的位移、速度和加速度与凸轮转角之间的关系为：

对于摆动从动件，上述公式同样成立，只需把公式中的位移、速度和加速度替换为角位移、角速度和角加速度即可。

（3）凸轮机构的压力角 凸轮机构的压力角是指不计摩擦时，凸轮与从动件在某瞬时接触点处的公法线方向与从动件运动方向之间所夹的锐角，常用表示。压力角是衡量凸轮机构受力情况好坏的一个重要参数，压力角越大，从动件所需的驱动力就越大，不但会加剧凸轮轮廓磨损，使机械传动效率降低，甚至可能会发生自锁，因此，在凸轮机构设计中，应保证。

2．从动件运动规律的选择与设计原则

在凸轮机构中，从动件的运动通常就是凸轮机构的输出运动，其运动规律与特性会直接影响到整个凸轮机构的运动学、动力学、精度、冲击、振动和噪声等特性。因此，正确地选择和设计从动件的运动规律，是凸轮机构设计的一项重要内容。

（1）基本运动规律 基本运动规律有如下两种种：

① 多项式类运动规律

多项式类运动规律的一般形式为

式中， 为待定系数，可根据凸轮机构工作要求所决定的边界条件确定。

在上述多项式运动规律中，常采用的是n＝1、n＝2以及n＝5时的三种多项式运动规律，分别称为一次多项式运动规律（也叫等速运动规律）、二次多项式运动规律（等加速等减速运动规律）和五次多项式运动规律。

② 三角函数类运动规律

三角函数类运动规律是指从动件的加速度按余弦规律或正弦规律变化。当从动件的加速度以余弦规律变化时，称为余弦加速度运动规律（也称简谐运动规律），以正弦规律变化时称为正弦加速度运动规律（也称摆线运动规律）。

表6-1列出了几种常用运动规律的运动特性、冲击特性和适用场合，供设计凸轮机构时参考。

表6-1几种常用运动规律的特性比较

运动规律				冲击特性	适用场合
等速运动规律	1			刚性冲击	低速、轻载
等加等减运动规律	2	4		柔性冲击	中速、轻载
多项式运动规律	1.88	5.77	60	无	高速、中载
简谐运动规律	1.57	4.93		柔性冲击	中速、中载
摆线运动规律	2	6.28	39.48	无	高速、中载

（2）组合型运动规律 在实际应用中，除了选用上面介绍的几种基本运动规律外，还可以选择其它类型的运动规律，也可以将几种不同的基本运动规律组合起来，形成新的组合型运动规律，可以改善凸轮机构的运动和动力特性，以满足工程实际中的多样化要求。例如，若要求从动件作等速运动，且在行程起点和终点处无任何形式的冲击，则可以等速运动规律为主体，在行程的起点和终点处用摆线运动规律或5次多项式运动规律来组合。再如，由等加速等减速运动规律和摆线运动规律组合而成的改进梯形加速度运动规律，具有最大加速度小、连续性和动力特性好等特点，适用于高速场合。通常，在选择组合使用运动规律时，应遵循以下原则：

① 按凸轮机构的工作要求选择一种基本运动规律作为主体运动规律，然后用其它运动规律与之组合，通过优化对比，寻求最佳的组合型式。

② 在行程的起点和终点处，有较好的边界条件。

③ 在运动规律的连接点处，根据不同的使用要求，应满足位移、速度、加速度甚至是更高一阶导数的连续条件，以减少或避免冲击。

④ 各段运动规律要有较好的动力特性。

（3）从动件运动规律的选择与设计原则 选择与设计从动件的运动规律是凸轮机构设计的一项重要内容。在进行运动规律的选择与设计时，不但要考虑凸轮机构的实际工作要求，还要考虑凸轮机构的工作速度和载荷的大小、从动件系统的质量、动力特性以及加工制造等因素。具体地讲，主要需要注意以下几点：

① 从动件的最大速度 应尽量小。越大，则最大动量越大，特别是当从动件系统的质量m较大时，过大的动量会导致凸轮机构引起极大的冲击力，因此应该限制从动件的最大速度。

② 从动件的最大加速度应尽量小，且无突变。由于从动件的惯性力为，因此，越大，机构的惯性力就越大。特别是对于高速凸轮，应该限制最大加速度 ，以减小机构惯性力的危害，而且对提高凸轮机构的动力性能也有很大的帮助。

③ 从动件的最大跃度应尽量小。跃度是加速度的一阶导数，它反映了惯性力的变化率，直接影响着机构的振动和运动平稳性，因此希望越小越好。

3．凸轮轮廓曲线的设计

凸轮轮廓曲线设计的主要任务是根据选定的从动件运动规律及其它设计参数，求解出凸轮的轮廓曲线。凸轮轮廓曲线的设计方法有作图法和解析法，但不管采用哪种方法，设计凸轮轮廓曲线的基本原理都是相同的，即相对运动原理。

（1）凸轮机构的相对运动原理（反转法原理） 在凸轮机构中，凸轮的转角j与从动件的位移s存在对应关系。现设想给整个凸轮机构加上一个绕凸轮回转中心O的反转运动，且使反转角速度的大小等于凸轮的角速度，即反转角速度为－。此时，凸轮与从动件之间的相对运动关系仍保持不变，但凸轮将静止不动，成为机架。对于直动从动件，一方面随导路绕O点以角速度－转动，同时又沿其导路方向按预期的运动规律作相对移动。而对于摆动从动件，则一方面随其摆动中心一起以角速度－转动，同时又绕从动件的摆动中心按预期的运动规律作相对摆动。由于从动件的尖底在相对运动过程中始终与凸轮轮廓曲线保持接触，因此，从动件尖底在由反转和相对移动组成的复合运动中的轨迹便形成了凸轮的轮廓曲线，这就是凸轮机构的相对运动原理，也称反转法原理。

（2）凸轮廓线设计的作图法 掌握了凸轮机构的反转法原理，采用作图法设计凸轮廓线就非常简单了。下面以偏置式直动尖底从动件盘形凸轮机构的凸轮廓线设计为例进行说明，其设计步骤如下：

① 选取适当比例尺，并根据已知条件画出基圆、偏距圆以及从动件的初始位置；

② 根据作图精度要求沿（－w）方向等分基圆，并根据从动件的运动规律，按各等分点所对应的凸轮转角计算出从动件相应的位移；

③ 分别过基圆上的各等分点做偏距圆的切线，即为从动件在各位置时的导路；

④ 对于每一位置，按照所选比例尺，从导路与基圆的交点开始，并沿导路方向向外量取线段，其长度等于第（2）步计算出来的从动件在该位置时的位移值，线段终点即为从动件的尖底在复合运动中的轨迹点；

⑤ 把从动件尖底在所有位置时的轨迹点光滑连接，即可得到所求的凸轮轮廓曲线。

对于直动滚子从动件盘形凸轮机构，可以把滚子的圆心看作是尖底从动件凸轮机构中从动件的尖底，并按上述方法求出滚子中心在复合运动中的轨迹曲线，称为凸轮的理论廓线。由于凸轮的实际廓线与理论廓线是等距曲线，其法向距离等于滚子的半径。因此，以凸轮理论廓线上的各点为圆心，滚子半径为半径做一系列滚子圆，其包络线即为凸轮的实际廓线。

对于直动平底从动件盘形凸轮机构，可把平底与导路方向线的交点作为尖底从动件的尖底，并根据反转法原理，得到该点在复合运动中的一系列轨迹点。然后，分别以这些点作平底，平底族的包络线即为凸轮的实际廓线。

对于摆动从动件盘形凸轮机构，需要注意的是，根据运动规律所计算出的是对应于凸轮各位置时的角位移。在利用反转法原理等分基圆时，摆动从动件的回转中心将一起绕凸轮回转中心反转。然后，再以摆动从动件在各位置时的回转中心为圆心，摆动从动件的长度为半径作圆弧与基圆有一系列交点，其与摆动从动件在各位置时的回转中心的连线即为摆动从动件在反转运动中的最低位置。最后，以摆动从动件在各位置时的回转中心为顶点，此最低位置为始边，向外量取角度，大小等于各位置时的角位移，从而可以得到一系列摆动从动件在复合运动中的轨迹点，光滑连接之，即可得到凸轮的轮廓曲线。

（3）凸轮廓线设计的解析法 用解析法进行凸轮廓线设计的主要任务是根据已确定的运动参数和几何参数，并利用凸轮机构的相对运动原理，建立起凸轮轮廓曲线与凸轮转角的函数关系，即凸轮廓线方程。下面以偏置式直动滚子从动件盘形凸轮廓线设计为例进行。

如图6-1a所示，在直动滚子从动件盘形凸轮机构上建立直角坐标系，原点O位于凸轮的回转中心。当从动件在1位置时，设滚子中心点为凸轮推程段理论廓线的起始点。当整个凸轮机构反转j角后，从动件到达2位置，点到达B点，此时，从动件的位移。从图上可以看出，从动件上B点的运动可以看作是由点先绕O点反转j角到达凸轮基圆上的B’点，然后，B’点再沿导路移动位移s到达B点。设凸轮机构的偏距为e，点的坐标为（），B点的坐标为（x, y），因此，利用坐标的旋转变换和平移变换，可求得B点的坐标为：

（6－1）

式中，，，代入式（6－1）并整理得：

（6－2）

式（6－2）即为凸轮的理轮廓线方程。

由前知，凸轮的实际廓线是圆心位于理论廓线上的一系列滚子圆族的包络线，如图6-1b所示，而且，滚子圆族的包络线应该有两条（和），分别对应于外凸轮和内凸轮的实际廓线，其法向距离等于滚子的半径。设过凸轮理论廓线上B点的公法线与滚子圆族的包络线交于A（或A’）点，则A（或A’）点也是凸轮实际廓线上的点。设A（或A’）点的坐标为（x_a， y_a），则凸轮的实际廓线方程为：

（6－3）

式中，为公法线与x轴的夹角，（x，y）为滚子圆圆心（位于理论廓线上）的坐标。需要说明的是，公式中上面一组符号用于求解外凸轮的实际廓线，下面一组符号用于计算内凸轮的实际廓线。

利用高等数学的知识，曲线上任意一点法线的斜率与该点处切线斜率互为负倒数，所以有：

（6－4）

对式（6－2）求导可得

（6－5）

综合式（6－4）、（6－5）可得：

4．凸轮机构基本尺寸的确定

（1）凸轮机构压力角的确定 以偏置式直动滚子从动件盘形凸轮机构为例，如图6-2所示，根据其中的几何关系，压力角求解公式为：

（6－6）

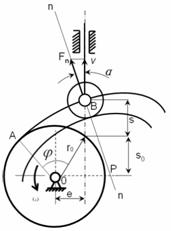
图6-2 直动从动件的压力角

式中，“”号与从动件的偏置方向有关。图示应该取“－”号，反之，如果从动件导路位于凸轮回转中心O的左侧，则应该取“＋”号。

也就是说，凸轮机构的压力角与凸轮基圆半径、偏距和从动件的偏置方向等有直接的关系。同时，这些参数之间又往往是互相制约的。例如，在其它参数不变的情况下，增大凸轮的基圆半径可以获得较小的压力角，从而可以改善机构的受力状况，但缺点是凸轮尺寸增大。反之，减小凸轮的基圆半径虽然可以获得较为紧凑的结构，但同时又使凸轮机构的压力角增大。压力角过大可能会导致驱动力急剧增大，凸轮轮廓严重磨损和效率迅速降低，甚至会发生自锁而无法运转。因此，为了使凸轮机构能够正常工作并具有较高的传动效率，设计时必须对凸轮机构的最大压力角加以限制，使其小于许用压力角，即。凸轮机构的许用压力角如表6-2所示。

表6-2 凸轮机构的许用压力角

封闭形式	从动件的运动方式	推 程	回 程
力封闭	直动从动件	[a]=
	摆动从动件	[a]=
形封闭	直动从动件	[a]=
	摆动从动件	[a]=

（2）凸轮基圆半径的设计 由式（6－6）可知， 当从动件的运动规律和偏距已知时，凸轮的基圆半径与压力角呈反比关系，即压力角a越大，基圆半径越小。因此，在确定凸轮基圆半径时应综合考虑以下因素：

① 在满足最大压力角的条件下，尽量减小基圆半径，从而可以使设计出的凸轮机构在满足压力角条件的同时，又能获得紧凑的结构尺寸。

② 考虑凸轮机构在结构、强度以及安装等方面的要求。

③ 对于直动平底从动件盘形凸轮，可按照“凸轮的全部廓线外凸”的条件来设计凸轮的基圆半径。

④ 对于应用于重要场合的高速凸轮，可采用CAE技术来优化凸轮的基圆半径。

（3）滚子半径的设计 在滚子从动件盘形凸轮机构中，凸轮的实际廓线是其理论廓线上滚子圆族的包络线，因此，其形状必然与滚子的半径大小有关。在设计滚子尺寸时，必须保证滚子同时满足运动特性要求和强度要求。

从运动特性要求考虑，凸轮机构不能发生运动的失真现象。比如，当凸轮的理论廓线外凸时，理论廓线上某点的曲率半径、实际廓线在对应点的曲率半径为以及滚子半径为三者之间的关系为：。当 ³ 时，则该点处将发生实际廓线的曲率半径为零或负值的情况，表明在该位置出现尖点，运动过程中容易磨损；或者实际廓线出现交叉，在包络加工过程中，廓线的交叉部分将会被切掉，从而导致机构的运动发生失真。因此，为了避免发生这种现象，要对滚子的半径加以限制。通常情况下，应保证：

从强度要求考虑，滚子半径应满足以下条件：

（4）平底长度的设计 在平底从动件盘形凸轮机构运动过程中，应能保证从动件的平底在任意时刻均与凸轮接触，因此，平底的长度应满足以下条件：

式中，为从动件平底中心到平底与凸轮廓线接触点之间的最大距离，为附加长度，由具体的结构而定，一般取mm。

（5）偏距的设计 从动件的偏置方向可直接影响凸轮机构压力角的大小，因此，在选择从动件的偏置方向时需要遵循的原则是：尽可能减小凸轮机构在推程阶段的压力角。一般情况下，从动件运动速度的最大值发生在凸轮机构压力角最大的位置。而且，适当增大偏距，有利于减小凸轮机构的压力角。

三、学习重点及难点

1．学习重点

（1）凸轮机构的基本名词术语及运动规律、压力角等概念

（2）从动件常用的运动规律及其选择与设计原则

（3）平面凸轮廓线设计的图解法与解析法

（4）确定凸轮机构的压力角、基圆半径、滚子半径等基本尺寸

2．学习难点

（1）凸轮机构的相对运动原理

（2）灵活应用相对运动原理求解凸轮机构的转角、位移和压力角等参数

四、例题精选

例题6-1 如图6-3所示偏置直动滚子从动件盘形凸轮机构中，凸轮以角速度ω逆时针方向转动。试求：

（1）画出理论轮廓曲线、基圆与偏距圆；

（2）标出凸轮图示位置压力角α₁和位移s₁以及转过150°时的压力角α₂ 和位移 s₂ 。

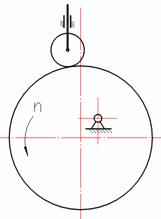
图6-3 例题6-1图

解：本题目主要考察对凸轮廓线、基圆、偏距圆、压力角及位移等基本概念的理解和对反转法原理的灵活运用。结果如图6-4所示：

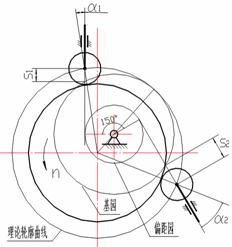
图6-4 例题6-1解图

例题6-2已知图6-5所示偏置式滚子从动件盘形凸轮机构。试求：

（1）标出基圆半径r₀？

（2）标出图示位置从动件位移s 和机构的压力角α ？

（3）求出r₀ 、s 和α之间的关系式？

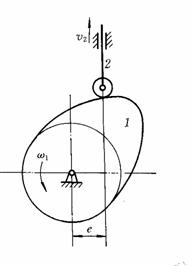
图6-5 例题6-2图

解：本题目主要考察对基圆、压力角及位移等基本概念的理解和压力角的计算方法。

（1）基圆半径r₀如图6-6所示。

（2）图示位置的s 和α如图6-6所示。

（3）r₀ 、s 与α之间的关系式为：

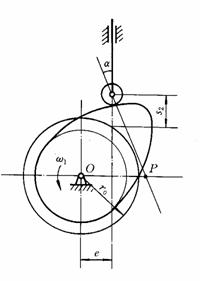
图6-6 例题6-2解图

例题6-3 如图6-7所示为摆动滚子从动件盘形凸轮机构，其中凸轮为偏心圆盘，且以角速度ω逆时针转动。试在图上标出：

（1）凸轮基圆；

（2）升程运动角F和回程运动角F¢；

（3）图示位置时从动件的初始位置角y₀和角位移y ；

（4）图示位置从动件的压力角α；

（5）从动件的最大角位移y_max 。

图6-7 例题6-3图

解：本题目主要考察对摆动从动件凸轮机构的基圆、行程运动角、压力角及角位移等基本概念的理解。结果如图6-8所示。

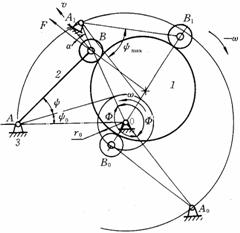
图6-8 例题6-3解图

五、试题自测及答案

1．填空题

（1）凸轮与从动件保持接触的方式有　　　　　　和　　　　　　　两种。

（2）在滚子从动件盘形凸轮机构中，凸轮的理论廓线与实际廓线之间的关系为　　　 　。

（3）凸轮机构的压力角是指 。

（4）在推程过程中，限制凸轮机构压力角的原因是　　　　　　　　　　　　。

（5）盘形凸轮的基圆半径是　　　　　　　　　　上距凸轮回转中心的最小向径。

（6）在设计滚子从动件盘形凸轮轮廓曲线时，若出现　　　　　　　　　　　　　　　时，会发生从动件的运动失真现象。此时，可采用　　　　　　　　 　　　　　　　方法来避免从动件的运动失真。

（7）用作图法绘制直动从动件盘形凸轮廓线时，常采用　　　　　法。即假设凸轮　　　　　　，从动件作　　　　　　　　　　　　　的复合运动。

（8）在对心直动尖顶从动件盘形凸轮机构中，若凸轮基圆半径增大，则其压力角将　　　　；在对心直动平底从动件盘形凸轮机构中，若凸轮基圆半径增大，则其压力角将　 　　　　　 。

2．选择题

（1）理论廓线相同、实际廓线不同的两个对心直动滚子从动件盘形凸轮机构，其从动件的运动规律　　。

A. 相同； B. 不相同。

（2）在设计直动滚子从动件盘形凸轮机构的实际廓线时，发现压力角超出了许用值，此时可采取的措施为 。

A. 减小滚子半径； B. 加大基圆半径； C. 减小基圆半径。

（3）在设计滚子从动件盘形凸轮机构时，轮廓曲线出现尖顶或交叉是因为滚子半径　　该位置理论廓线的曲率半径。

A. >； B. <； C. ； D。

（4）对于转速较高的凸轮机构，为了减小冲击和振动，从动件最好采用　　运动规律。

A. 等速； B. 等加速等减速； C. 正弦加速度。

（5）在凸轮机构中，从动件以等加速等减速运动规律运动时存在　　冲击。

A. 刚性； B. 柔性； C. 无。

（6）当凸轮基圆半径相同时，从动件采用适当的偏置方向可以　　　　凸轮机构推程的压力角。

A. 减小； B. 增加； C. 保持原来。

3．如图6-10所示偏置直动滚子从动件盘形凸轮机构中，凸轮以角速度逆时针方向转动。试求：

（1）画出理论轮廓曲线、基圆与偏距圆；

（2）标出凸轮从图示位置转过90°时的压力角和从动件的位移s。

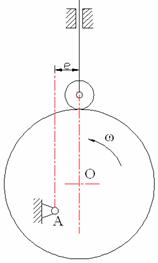
图6-10 题3图

4．如图6-11所示一对心直动尖顶从动件偏心圆凸轮机构，O为凸轮几何中心，O₁为凸轮转动中 心，直线AC^BD，O₁O=OA，圆 盘 半 径 R=60 mm。 试计算：

（1）根据图6-11a及上述条件确定基圆半径r₀、行程h，C点压力角α_C和D点接触时的位移s_D 、压力角α_D 。

（2）若偏心圆凸轮的几何尺寸不变，仅将从动件由尖顶改为滚子（图6-11b），滚子半径r_T=10mm。试问上述参数r₀ 、h、 α_C和s_D 、α_D有无改变？如有改变，计算其数值。

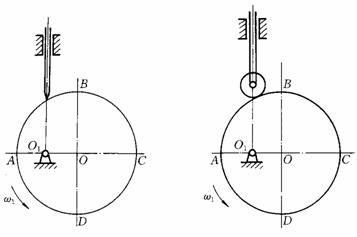
a) b)

图6-11 题4图

5．如图6-12所示凸轮机构中，凸轮为一偏心圆盘，圆盘半径R=80mm，圆盘几何中心O到回转中心A的距离OA=30mm，偏距e=15mm，平底与导路间的夹角β＝45°，凸轮以等角速度w=1 rad/s逆时针回转。试计算：

（1）凸轮实际廓线的基圆半径 r_b；

（2）从动件的行程 h；

（3）该机构的最大压力角α_max与最小压力角α_min；

（4）从动件的推程运动角F和回程运动角F¢；

（5）从动件的最大速度v_max。

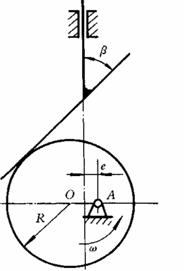
图6-12 题5图

6．如图6-13所示为一偏置直动滚子从动件盘形凸轮机构，凸轮为偏心圆盘，其直径D=42mm，滚子半径 r_T=5 mm，偏距 e=6 mm。试求：

（1）画出基圆，并计算基圆半径；

（2）画出凸轮的理论廓线；

（3）确定从动件的行程 h；

（4）确定从动件的推程运动角F及回程运动角F¢；

（5）说明该机构在运动中有无失真现象，为什么？

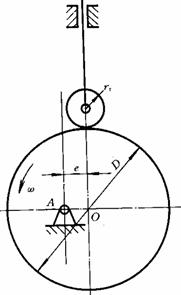
图6-13 题6图

7．如图6-14所示为一摆动滚子从动件凸轮机构。 试在图上标出：

（1）从C点接触到D点接触过程中，凸轮转角j和从动件摆角y ；

（2）在D点接触时的压力角α。

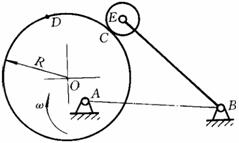
图6-14 题7图

8．如图6-15所示为摆动滚子从动件圆盘凸轮机构，现已知：圆盘半径R、圆心与转轴中心的距离L_OA＝R/2和滚子半径r_T。试求：

（1）标出在图示位置时的压力角α与推杆的摆角y ；

（2）画出滚子推杆的最大摆角y_max ；

（3）当α> [α] 时，对凸轮机构有何影响，如何使压力角减小？

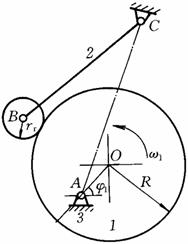
图6-15 题8图

参考答案

1． 填空题

（1）力封闭；形封闭

（2）法向距离恒等于滚子半径

（3）凸轮与从动件在某瞬时接触点处的公法线方向与从动件运动方向之间所夹的锐角

（4）提高机械效率、改善受力情况

（5）凸轮的理论廓线

（6）滚子半径大于理论廓线上的最小曲率半径；加大凸轮基圆半径或减小滚子半径

（7）反转法；静止不动；绕凸轮回转轴线的反向转动和沿从动件导路方向的往复移动

（8）减小；保持不变

2． 选择题

（1）A；（2）B；（3）D；（4）C；（5）B；（6）A。

3．解：

结果如图6-16所示。

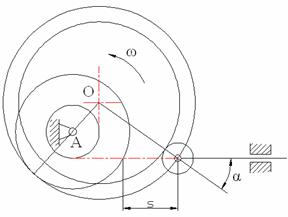
图6-16 题3解图

4．解：

利用反转法，作图结果如图6-17所示。

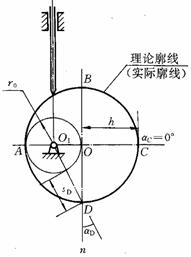
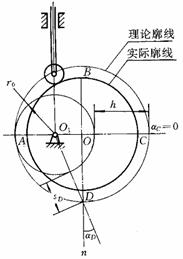
a) b)

图6-17 题4解图

（1）在图6-17a中

（2）在图6-17b中

5．解：

利用反转法，作图结果如图6-18所示。

（1）

（2），

所以，。

（3）

（4）F＝F¢＝180°

（5）当凸轮从从动件最低位置转过90°时，从动件与凸轮的相对瞬心P至A点的距离达到最大。

所以，。

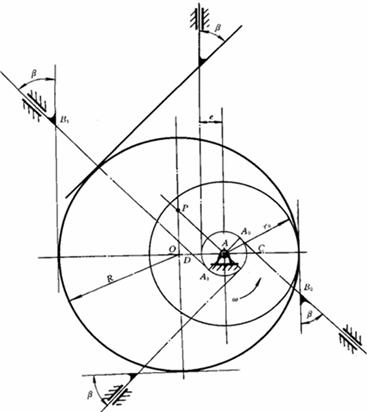
图6-18 题5解图

6．解：

利用反转法，作图结果如图6-19所示。

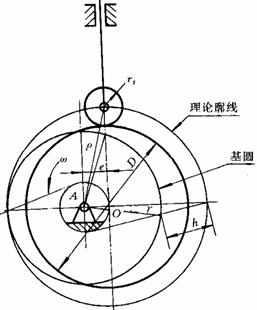
图6-19 题6解图

（1）

（2）理论廓线如图示

（3）因为，

所以

（4）因为

所以

（5）无失真现象。因凸轮廓线外凸且处处曲率半径相等，均为R=21mm，并有r_T=5mm＜R，故不会发生失真现象。

7．解：

结果如图6-20所示。

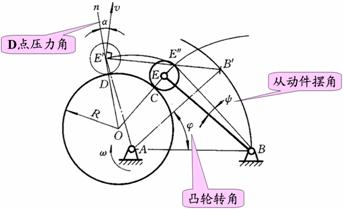
图6-20 题7解图

8．解：

结果如图6-21所示。

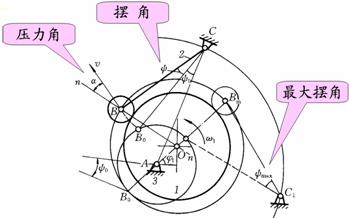
图6-21 题8解图

（3）当α>[α]时，推动摆杆运动的有效分力减小，机械效率降低，甚至发生自锁。可通过增大基圆 半径的方法减小压力角。