一、实验目的：

演示两个衍射图像能被分辨的瑞利判据

二、实验原理：

在光学仪器中，通常使用透镜。过去处理透镜问题是以几何光学为基础的，按照光的直线传播，不论两个物点多么靠近，通过透镜总可以得到两个分开、清晰可辨的像点。但是，几何光学是波动光学的一个近似。按照波动光学，衍射现象是不可避免的。因此，一个物点通过透镜所成的像不是一个几何点，而是一个衍射图样。如果两个物点因为距离过近，而使它们通过光学仪器后形成的衍射图样发生了较大的重叠，这两个物点就不能被光学仪器所分辨。由此可见，衍射现象限制了光学仪器的分辨本领。由于在光学仪器中使用较多的孔径光阑和透镜都是圆形的，因此，光通过孔径光阑或透镜的衍射相当于光通过圆孔的衍射。下图是夫琅和费圆孔衍射的实验装置示意图。当单色平行光垂直照射到圆孔上时，衍射光经过透镜，在位于透镜的焦平面处的观察屏E上形成衍射图样。衍射图样中央是一个较亮的圆斑，称为爱里(G.B.Airy)斑，衍射光的大部分能量将集中在爱里斑中。爱里斑的外围是一组明、暗相间亮度减弱的同心圆环。

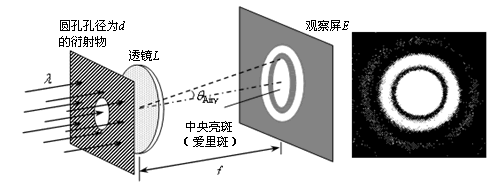
夫琅和费圆孔衍射的实验示意图

这里爱里斑的大小，由其周围的一级暗环所对应的衍射角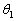决定。计算可得：

第一级暗环的衍射角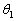满足下式

式中r和d分别是圆孔的半径和直径。

爱里斑的角半径qAiry就是第一级暗环的衍射角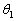。当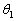很小时，qAiry为

 

设透镜的焦距为f，由于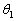很小，故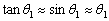，则爱里斑的半径RAiry为

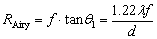
这种圆孔衍射将对光学仪器的分辨本领产生较大的影响。现在以圆形透镜为例来说明光学仪器的分辨本领与哪些因素有关。设很远处有两个点光源s1和s2，它们各自发出的光(可看成平行光)通过透镜，在透镜的焦平面上形成两个爱里斑衍射图样。如果点光源s1和s2之间的距离较远，它们通过透镜产生的爱里斑因距离较远而能够完全分开，它们的像就容易被分辨。如果两个点光源s1和s2逐渐靠近，它们形成的爱里斑也将逐渐靠近，并开始发生重叠，它们的像就变得较不容易被分辨。瑞利(Rayleigh)对此提出了一条两个爱里斑衍射图样恰好能被分辨的判据：如果两个爱里斑的中心间距大于或等于爱里斑的半径，如下图（a）所示，两个爱里斑像就可分辨或恰可分辨；如果两个爱里斑的中心间距小于爱里斑的半径，如下图 (c)所示，两个爱里斑像就不能分辨。

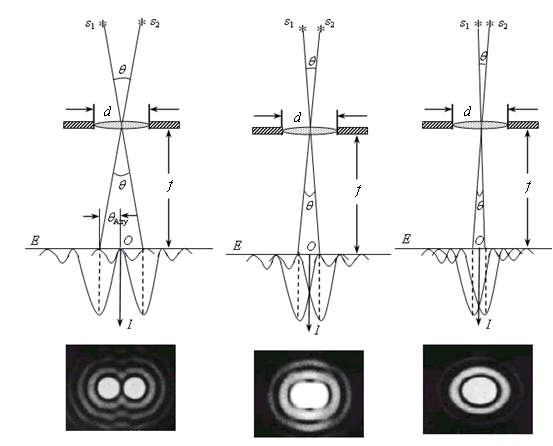
(a)(b)(c)

图16-7 两个衍射图样能被分辨的瑞利判据

(a) 当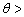qAiry时，可分辨；(b) 当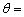qAiry时，恰可分辨；(c) 当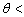qAiry时，不可分辨

设两个点光源对透镜光心的张角为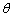。由瑞利判据可知，“恰可分辨”的两个点光源的衍射图样中心之间的距离应等于爱里斑的半径。此时，两点光源对透镜光心的张角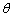应等于爱里斑的角半径qAiry，即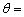qAiry。所以，爱里斑的角半径qAiry也称为最小分辨角如图(b)所示，以qmin表示。由此可得最小分辨角qmin的大小表示为

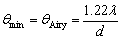
在光学仪器中，通常用最小分辨角qmin的倒数来表征分辨本领的大小，又称为分辨率，用R表示。于是，光学仪器的分辨本领为

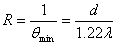
由上式可知，分辨本领与波长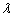成反比，与通光孔径或透镜的直径d成正比。因此，为了清楚地观察远方的星体，天文望远镜总是用直径很大的透镜作为物镜，以提高望远镜的分辨本领。而在显微镜中，常使用波长较短的紫光照明，来提高显微镜的分辨本领。