 |
一、实验目的：
演示一维无限深方势阱中粒子的能级、波函数、概率密度与量子数n的关系
二、实验原理：
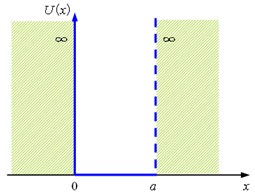
无限深方势阱是一种简单的理论模型。金属中的自由电子的运动，就可以粗略地利用这一模型，以解释金属的物理性质。由于金属材料表面的自由电子，需要克服逸出功才能逸出金属表面。因此对于电子来说，在金属外的势能要比在金属内高。作为一个理想模型，可以认为电子是处于以金属表面为边界的无限深方势阱中。
如图所示，一维无限深方势阱的势能表达式为
在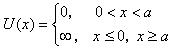
和
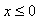区域，势能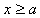
。物理上势能为无穷大的含义是，具有有限能量的粒子不能出现在该区域。因此
；
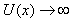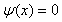
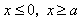在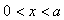
区域，即势阱内，势能
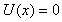，说明粒子不受力而自由运动。此时一维定态薛定谔方程可写成
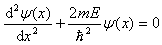
其中，m为粒子的质量，E是粒子的总能量。令
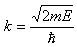
则一维定态薛定谔方程可写成
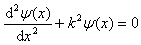
上式是一个二阶常系数微分方程，解上式，并利用单值、连续、有限的标准条件和归一化条件可得
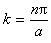；n=1，2，3，……
定态波函数为
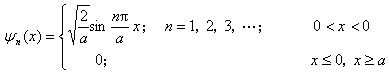
一维无限深方势阱中粒子的能量为
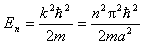；n=1，2，3，……
其中，n称为量子数。
通常把在无限远处为零的波函数所描述的状态称为束缚态。上式表明，当粒子被束缚在无限深势阱中，粒子的能量不能连续取值，只能取一系列分立值，称为能级。这一结果与经典粒子完全不同。在经典力学中，粒子的能量可连续取值；而量子力学的结果是，粒子的能量是量子化的。且在求解薛定谔方程得到定态波函数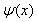
的同时，自然而然地确定了能量的允许取值，而不需要像量子论初期那样，以人为假设的方式引入。这样的问题在数学中称为本征值问题，
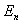称为能量本征值，
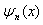称为与能量本征值
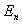对应的本征波函数。
当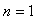
时，粒子处于最低能量状态，称为基态。基态能量为
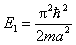
即它不等于零，称为零点能，表明在阱中的粒子永远不能静止。
当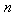
取不等于1的其它值时的能量状态称为激发态，其能量
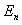是基态能量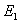
的
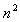倍，即
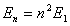
由上式可看出，相邻两个能级之差即能级间隔为
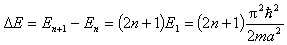
以及有
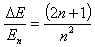
虽然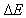
随n的增加而越来越大，但是
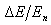随n的增加而越来越小；当
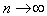时，能量变为连续的。另外，当粒子质量m和阱宽a越大，
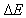越小；所以对于宏观尺度的物体质量m和阱宽a来说，能量可看作连续变化，这和经典物理相对应。因此，能量量子化只是微观世界的特征。
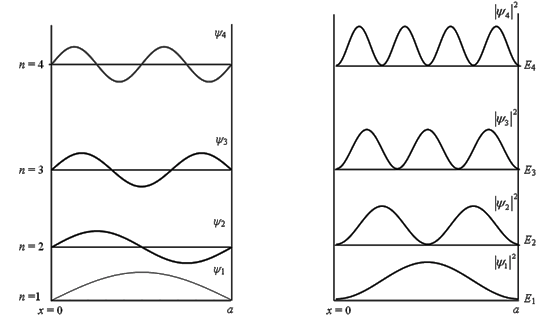
下图给出在一维无限深方势阱中，对应于粒子前三个能级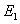
、
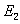>和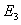
的定态波函数
、
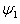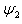和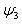
以及相应的概率密度
、
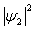和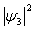
。由图可见，每一个能量本征态
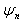都对应德布罗意波的一个特定波长的驻波。在有限的空间内，微观粒子的波在势阱边缘来回反射并叠加，以驻波形式稳定地存在着。例如，当粒子处于
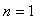的能级时，波函数为
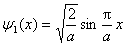
其形状就是节点在阱边缘(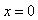
，a)处的包含半个德布罗意波长的驻波。容易求得处于基态的粒子动量为
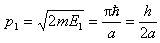
由德布罗意关系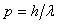
，可得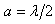
。所以一维无限深势阱中的粒子的定态物质波相当于两端固定的弦中的驻波。波长
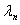满足
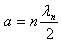，n=1，2，3，……
即势阱宽度a必须等于德布罗意波的半波长的整数倍。
根据波函数的物理意义，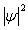
为粒子在各处出现的概率密度，它的数学表示为
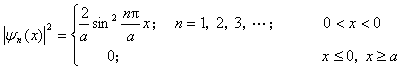
由图可见，粒子在势阱中的概率分布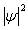
是不均匀的，随x改变，与n有关，而且有若干概率为零的节点。这一点与经典力学很不相同。按照经典力学，粒子在势阱内的运动是不受限制的，粒子在阱内各处出现的概率就应当是相等的。
微观粒子在势阱中运动的现象是较为常见的，例如在核(线度1.0×10-14 m)内的质子和中子可以当成处于无限深的势阱中而不能逸出，它们在核中的运动是自由的。